- 一般項
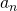 が分母に
が分母に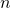 を含む分数の形で表される数列の和を求める問題です。
を含む分数の形で表される数列の和を求める問題です。 - 出題形式には
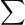 を用いて一般項が表される形と、初項からいくつかの項が書き表される形があります。
を用いて一般項が表される形と、初項からいくつかの項が書き表される形があります。 - 部分分数分解を用いて
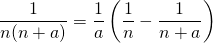 と変形し、数が同じで符号が異なるものを消していきます。
と変形し、数が同じで符号が異なるものを消していきます。
スポンサーリンク
分数の数列の和を求める問題
![]()
を求めなさい。
分数の数列の和を求める解法の手順
- 部分分数分解を用いて、分数を2つに分けて表します。
- 項を実際に書き並べます。
- 数が同じで符号が異なるもの同士を足すことで消し、残ったものを足します。
分数の数列の和を求める問題の解説
分母が2つの数の積として表されているので、
部分分数分解を用いて分母が1つの数だけで表される形に変形します。
![]()
より
![]()
となるので、
![]()
![Rendered by QuickLaTeX.com \[=\dfrac{1}{2} \Biggl(\left(\dfrac{1}{1}-\dfrac{1}{3} \right)+\left(\dfrac{1}{2}-\dfrac{1}{4} \right) +\left(\dfrac{1}{3}-\dfrac{1}{5}\right) +\left(\dfrac{1}{4}-\dfrac{1}{6}\right) +\dots +\left(\dfrac{1}{n}-\dfrac{1}{n+2}\right)\Biggr)\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-afdb116b916887b0d058fc83b2f0a123_l3.png)
と変形できます。
この中で、初項を分解してできた![]() と第3項を分解してできた
と第3項を分解してできた![]() のように、
のように、
数が同じで符号が異なるものを消すことで、和が求められます。
初めのうちは多めに項を書くようにすると、消える部分と残る部分が考えやすくなります。
![Rendered by QuickLaTeX.com \[\dfrac{1}{2} \Biggl(\left(\dfrac{1}{1}-\dfrac{1}{3} \right)+\left(\dfrac{1}{2}-\dfrac{1}{4} \right) +\left(\dfrac{1}{3}-\dfrac{1}{5}\right) +\left(\dfrac{1}{4}-\dfrac{1}{6}\right) +\dots +\left(\dfrac{1}{n}-\dfrac{1}{n+2}\right) \Biggr)\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-9ecaafaac3a2573361eb2ffef5fdccc7_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{1}{2} \Biggl(\dfrac{1}{1}+\dfrac{1}{2}+\left(\dfrac{1}{3}-\dfrac{1}{3} \right)+\left(\dfrac{1}{4}-\dfrac{1}{4} \right) +\dots +\left(\dfrac{1}{n}-\dfrac{1}{n}\right) -\dfrac{1}{n+1}-\dfrac{1}{n+2} \Biggr)\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-6cb044708df75d5bfe1ac9dfa7b5d85b_l3.png)
![]()
![Rendered by QuickLaTeX.com \[=\dfrac{1}{2} \Biggl(\dfrac{2(n+1)(n+2)}{2(n+1)(n+2)}+\dfrac{(n+1)(n+2)}{2(n+1)(n+2)}-\dfrac{2(n+2)}{ 2(n+1)(n+2)}-\dfrac{2(n+1)}{ 2(n+1)(n+2)} \Biggr)\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-cf953199e6c42e3c73cf743f0ef4e8c5_l3.png)
![]()
![]()
より、和は ![]() となります。分子が因数分解できる形になったので分子、分母ともに
となります。分子が因数分解できる形になったので分子、分母ともに
因数分解した形で表しましたが、両方とも展開した形で解答しても構いません。
参考
チャート式 数研出版