スポンサーリンク
3次の三角関数の最大値・最小値を求める問題のポイント
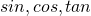 が含まれる、3次以上の関数の最大値や最小値を求める問題です。
が含まれる、3次以上の関数の最大値や最小値を求める問題です。 - 三角関数を他の文字に置き換えて微分します。
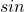 と
と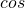 の和・差が含まれる場合、和・差をそのまま他の文字に置き換えます。
の和・差が含まれる場合、和・差をそのまま他の文字に置き換えます。 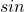 と
と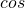 の積は、相互関係を利用して和・差に変形します。
の積は、相互関係を利用して和・差に変形します。
3次の三角関数の最大値・最小値を求める問題
![]() の最大値と最小値を求めなさい。
の最大値と最小値を求めなさい。
3次の三角関数の最大値・最小値を求める解法の手順
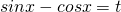 と置きます。
と置きます。 - 相互関係を利用して、
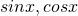 を
を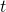 を用いて表します。
を用いて表します。 - 1、2から
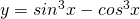 を
を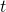 を用いて表します。
を用いて表します。 - 合成を利用して、
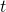 の値の範囲を求めます。
の値の範囲を求めます。 - 微分を利用して、3で求めた範囲での増減を調べます。
- 極値と定義域の両端での値を比較し、最大値と最小値を求めます。
3次の三角関数の最大値・最小値を求める問題の解説
三角関数を含む関数の場合、三角関数を他の文字に置き換えることで微分が簡単になります。
sinとcosの和・差が含まれる場合、合成によってsinだけで表すことができるので
和・差をそのままで文字に置き換えます。
まず、![]() と置きます。与えられた関数は
と置きます。与えられた関数は
![]()
![]()
![]()
となるので、![]() を
を![]() を用いて表すことができれば、
を用いて表すことができれば、
![]() を
を![]() を用いて表すことができます。
を用いて表すことができます。
![]() の両辺を2乗すると
の両辺を2乗すると
![]()
となり、相互関係より![]() なので
なので
![]()
と表せます。よって、
![]()
![]()
![]()
![]()
と表せます。ここで、変数が![]() から
から![]() に置き換わったので
に置き換わったので![]() の値の範囲を求めます。
の値の範囲を求めます。
三角関数の合成を利用すると、
![]()
![Rendered by QuickLaTeX.com \[=~\sqrt[]{\mathstrut 2} \left( \dfrac{1}{~\sqrt[]{\mathstrut 2} } sin x-\dfrac{1}{~\sqrt[]{\mathstrut 2}} cos x \right)\]](http://text.yarukifinder.com/wp/wp-content/ql-cache/quicklatex.com-8c4040625f5a1dc28ecae0d4386d9896_l3.png)
![]()
となるので、 ![]() より
より
![]()
![]()
よって、
![]()
となります。 ![]() の値の範囲が求められたので、この範囲での関数の増減から、最大値と最小値を求めます。
の値の範囲が求められたので、この範囲での関数の増減から、最大値と最小値を求めます。
![]()
より
![]()
![]()
となるので、![]() の値に対する
の値に対する![]() の増減は以下のようになります。
の増減は以下のようになります。
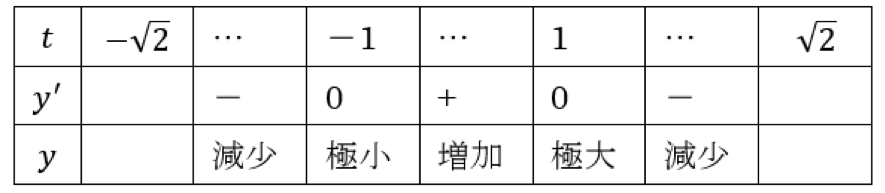
増減表
![]() のとき
のとき
![]()
![]() のとき
のとき
![]()
![]() のとき
のとき
![]()
![]() のとき
のとき
![]()
となるので、 最大値2、最小値-1と求められます。
参考
チャート式 数研出版