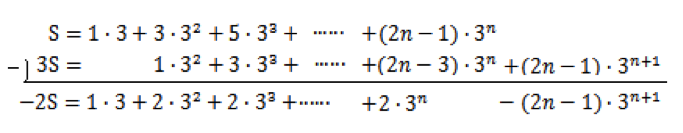- 一般項が
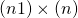 で表される、等差数列と等比数列の積の数列の和を求める問題です。
で表される、等差数列と等比数列の積の数列の和を求める問題です。 - 数列の和
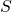 に、等比の部分の公比
に、等比の部分の公比 をかけた数列の和
をかけた数列の和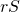 を求めます。
を求めます。 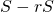 を、項を1つずつずらした形で求めます。
を、項を1つずつずらした形で求めます。 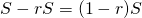 は等比数列になるので、等比数列の和の公式を用いて和が求められます。
は等比数列になるので、等比数列の和の公式を用いて和が求められます。
スポンサーリンク
等差数列と等比数列の積の和の問題
![]() の一般項を求めなさい。
の一般項を求めなさい。
Snと置き一般項を導く解法の手順
- 与えられた和をSと置きます。
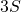 を求めます。
を求めます。 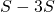 を、項を1つずつずらして求めます。
を、項を1つずつずらして求めます。 - 等比数列の和の公式から、
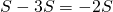 を求めます。
を求めます。 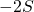 の値から、
の値から、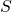 を求めます。
を求めます。
等差数列と等比数列の積の和の問題の解説
![]()
と置きます。
この式は、等差数列![]() と等比数列
と等比数列![]() の積で表される数列の
の積で表される数列の
第![]() 項までの和であると考えられます。
項までの和であると考えられます。
等比数列の和の公式と同様に、等比の部分の公比である![]() をかけた
をかけた![]() を求めると、
を求めると、
![]()
となります。
この式をSから項を1つずつずらして引くことで、等差の部分が消去できます。
和の様子
得られた
![]()
について、
![]() の部分は初項
の部分は初項![]() 、公比3、
、公比3、
![]() より項数
より項数![]() の等比数列の和となるので、
の等比数列の和となるので、
![]()
![]()
![]()
となります。
よって、
![]()
![]()
![]()
![]()
となります。よって、
![]() の両辺を
の両辺を![]() で割ることで、
で割ることで、
![]()
が得られます。
参考
チャート式 数研出版