x軸との交点から二次関数を決定する問題のポイント

2016/3/4 2016/3/13 2次関数と方程式・不等式, 二次関数, 数学, 数学Ⅰ

スポンサーリンク

x軸との交点から二次関数を決定する問題のポイント

与えられた 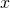$x$ 軸との交点を利用して二次関数を求める問題です。
因数分解された形である 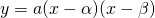$y=a(x-\alpha )(x-\beta )$ を利用することで簡単に求められます。
x軸と2点 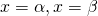$x=\alpha,x=\beta$ で交わるとき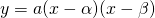 $y=a(x-\alpha)(x-\beta)$
x軸と1点 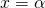$x=\alpha$ で交わるとき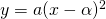 $y=a(x-\alpha)^2$

x軸との交点から二次関数を決定する問題

グラフが $(2,0),(-4,0),(3,7)$ の3点を通る二次関数を求めよ。

x軸との交点から二次関数を決定する解法の手順

x軸との交点である2点の座標から、 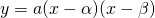$y=a(x-\alpha )(x-\beta )$ の形で二次関数の式を表します。
残る1点の座標を代入してaの値を求めます。
求められた二次関数は展開した形で表します。

x軸との交点から二次関数を決定する問題の解説

与えられた3点のうち、 $(2,0),(-4,0)$ はy座標が $0$ なので
x軸との交点であることがわかります。
この2点でy座標が $0$ となることから、求める2次関数の式は

$y=a(x-2)\Bigl(x-(-4)\Bigl)$

$y=a(x-2)(x+4)$

と表せます。この二次関数のグラフが点 $(3,7)$ を通るので、座標を代入すると

$7=a(3-2)(3+4)$

$7=7a$

$a=1$

となるので、求める二次関数は $y=1∙(x-2)(x+4)$ となります。よって、これを展開して

$y=x^2+2x-8$

となります。
$y=(x-2)(x+4)$ としても間違いではありませんが、展開を済ませた形で答えるのが一般的です。

参考

数研出版　チャート式

関連記事

スポンサーリンク