スポンサーリンク
指数方程式の解法ポイント
- 変数
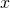 が累乗の指数の部分に含まれる、指数方程式を解く問題です。
が累乗の指数の部分に含まれる、指数方程式を解く問題です。 - 指数の底を揃え、
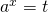 と置き換えることで、通常の方程式と同じように解くことができます。
と置き換えることで、通常の方程式と同じように解くことができます。 - (自然数のx乗)>0なので、解の範囲が限られることに注意します。
指数方程式の問題
指数方程式![]() を解きなさい。
を解きなさい。
指数方程式の解法の手順
- 指数の底を揃えます。
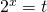 と置いて、式を
と置いて、式を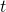 の2次方程式に書き換えます。
の2次方程式に書き換えます。 - 2次方程式を解いて
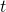 の値を求めます。
の値を求めます。 - 得られた
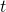 の値について
の値について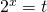 が成り立つかを確かめ、
が成り立つかを確かめ、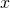 の値を求めます。
の値を求めます。
指数方程式の解説
3つ以上の項を含む指数方程式を解く際には、![]() と置き換えることで計算が簡単になります。
と置き換えることで計算が簡単になります。
置き換えの準備段階として、まずは指数の底を揃えます。
![]() なので、
なので、
![]()
を次のように変形できます。
![]()
また、![]() のままでは置き換えにくいので、
のままでは置き換えにくいので、
![]() より
より ![]() を
を
![]()
と変形し、
![]() として式全体を書き換えます。
として式全体を書き換えます。
![]() より
より![]() なので、
なので、 ![]() は
は
![]()
と書き換えられます。
このtの2次方程式を解くと、
![]()
より![]() が得られます。
が得られます。
ここで、得られたtの値について![]() を満たす
を満たす![]() が存在するかを確かめると、
が存在するかを確かめると、
![]() なので、
なので、![]() は
は![]() を満たす
を満たす![]() が存在せず、解として不適となります。
が存在せず、解として不適となります。
よって、解は![]() のみとなります。
のみとなります。
最後に![]() から
から![]() の値を求めると、対数の定義
の値を求めると、対数の定義![]() より
より
![]()
となります。
参考
チャート式 数研出版