恒等式を利用して、多項式の割り算の余りを求める問題のポイント：式と証明

恒等式を利用して、多項式の割り算の余りを求める問題のポイント

整式の除法の結果から、別の整式で割った余りを求める問題です。
(割られる整式)＝(割る整式)×(商)＋(余り)から恒等式を導き、解きます。

多項式の割り算の余りを求める問題

ある整式を $x-2$ で割ると $1$ 余り、 $(x+1)^2$ で割ると $2x-11$ 余った。
この整式を $(x-2) (x+1)^2$ で割ったときの余りを求めなさい。

恒等式を利用して、多項式の割り算の余りを求める解法の手順

割られる整式を 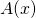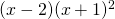$A(x)$ 、 $(x-2) (x+1) ^2$ で割ったときの商を 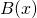$B(x)$ と置きます。
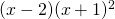$(x-2) (x+1)^2$ で割ったときの余りを、文字を使って表します。
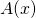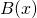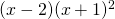$A(x)$ を $B(x)$ , $(x-2) (x+1) ^2$ と余りを使って表します。
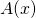$A(x)$ を、与えられた除法の結果を利用して表します。
3と4で表した式は恒等式になっているので、これを解きます。

多項式の割り算の余りを求める問題の解説

恒等式を利用することで、元の整式を求めずに余りを求めることができます。
ある整式を $A(x)$ とします。 $(x-2) (x+1)^2$ で割ったときの商を $B(x)$ と置きます。
$(x-2) (x+1)^2$ は3次式なので、 $(x-2) (x+1)^2$ で割ったときの余りは
$ax^2+bx+c$ と表せます。(余りが1次式の場合は $a=0$ 、定数の場合は $a=b=0$ となります。)
(割られる整式)＝(割る整式)×(商)＋(余り) となるので、

となります。

次に、与えられた除法の結果を式で表します。
$A(x)=B(x)(x-2) (x+1)^2+ax^2+bx+c$ を $(x+1)^2$ で割ったときの余りを考えると、
$B(x)(x-2) (x+1)^2$ は $(x+1)^2$ を因数に含むので、 $(x+1)^2$ で割り切れます。
よって、 $B(x)(x-2) (x+1)^2+ax^2+bx+c$ を $(x+1)^2$ で割ったときの余りは
$ax^2+bx+c$ を $(x+1)^2$ で割ったときの余りと等しくなります。